Curva di interazione suolo-struttura - ssi_py
Si tratta di un modello dinamico nonlineare di interazione terreno-struttura (SSI), sviluppato e realizzato da Allotey and El Naggar [2005a; 2005b], adatto all'analisi di fondazioni, muri di sostegno e pali sotto diversi regimi di carico (la nomenclatura scelta per questa curva mette in evidenza il fatto che questo modello può essere utilizzato per effettuare analisi laterali su pali, dove sono comunemente impiegate le curve p-y). Questo modello considera la formazione di gap con la possibilità di considerare il "crollo" del suolo; è caratterizzato da un incrudimento/degrado ciclico per effetto di un carico di ampiezza variabile, e infine può modellare risposte confinate, o meno, all'interno delle loro curve dorsali iniziali. L'incrudimento/degrado ciclico dovuto alla pressione dei pori e ai cambiamenti volumetrici è rappresentato mediante l'utilizzo di funzioni di danno ellittiche, implementate all'interno del modified rainflow counting algorithm [Anthes, 1997]; è anche impiegato l'approccio del numero equivalente di cicli [es. Seed et al. 1975; Annaki and Lee, 1977]. L'effetto del crollo del suolo è, invece, modellato utilizzando una funzione iperbolica sviluppata empiricamente.
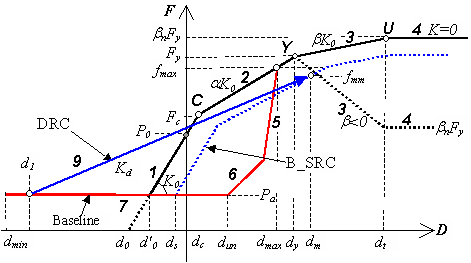
È evidente che questo modello isteretico, da solo, non è sufficiente a modellare un dato sistema di fondazioni. Pertanto, è necessario utilizzare una serie di molle (link), caratterizzate da una curva ssi_py opportunamente calibrata, in associazione, di solito, con un elemento trave-colonna. In altre parole, questa curva di risposta è da impiegare nella modellazione di fondazioni alla Winkler nonlineari (BNWF), in cui vengono impiegate una serie di molle sotto le fondazioni e per ciascuna di queste devono essere fornite le curve di risposta. Per un plinto i parametri sono gli stessi per tutte le molle, mentre per un palo, o un muro di sostegno, i parametri variano con la profondità, in quanto il sovraccarico aumenta con la profondità.
Inoltre, come notato qui, all'elemento link può essere assegnato uno smorzamento viscoso ogni volta che l'utente desideri, in qualche modo, tener conto degli effetti di "radiation damping" (questo sarà come introdurre un elemento dashpt parallelo alla molla che modella il suolo). Gli utenti possono fare riferimento alla letteratura [ad esempio Wolf, 1994; Allotey and El Naggar, 2005b] per indicazioni su come calcolare i valori appropriati di smorzamento in funzione delle caratteristiche di vibrazione del sistema suolo-struttura. Comunemente, se il periodo di vibrazione del sistema suolo-struttura è inferiore a quello del sito, allora gli effetti di "radiation damping" possono essere considerati trascurabili.
Per caratterizzare completamente la curva di risposta devono essere definiti diciannove parametri:
1° e 2° segmento della curva dorsale (K0, Fc, Fy, 
)
Il modello idealizza le relazioni di forza-spostamento del terreno in curve multi-lineari. Il primo segmento della curva dorsale ha una rigidezza iniziale K0. Il secondo segmento della curva inizia ad una forza Fc (definita come rapporto di Fy), con la rigidezza ridotta a 
. Il secondo segmento termina in corrispondenza della forza di snervamento del terreno Fy. I parametri di input variano come segue: 0 
Fc < 1, e 0.001 1. Per default, Fc = 0.5, = 1, e la definizione di Fc 
1 o 1 si traduce nel ripristino di Fc e ai loro valori di default.
3° e 4° segmento — curva finale (
and 
)
Il parametro di rigidezza (che definisce la rigidezza del 3° segmento in rapporto a K0) e il parametro della resistenza (che definisce la resistenza ultima in rapporto a Fy) determinano il comportamento finale della curva dorsale. La pendenza del terzo segmento può essere sia positiva che negativa (cioè si può avere un comportamento sia di hardening che di softening). La pendenza positiva non può essere maggiore della seconda pendenza del terreno, cioè un requisito è che sia minore di (questo è verificato nel programma come 0.9). Per < 0, il valore assoluto della pendenza non può essere maggiore della pendenza iniziale, cioè 
.
La seconda porzione della curva finale ha sempre una pendenza nulla. La resistenza in prossimità del punto di cambio pendenza tra la terza e la quarta porzione può essere specificata dal parametro (0). Nello specifico, < 1 per < 0, = 1 per = 0, e > 1 per > 0. Di default, = 1 con = 0, e la curva finale rappresenta una porzione della linea orizzontale. L'inserimento di > 0 e 1 o viceversa si traduce nel ripristino di entrambi i parametri ai valori di default.
Nel caso di una curva finale caratterizzata da una pendenza negativa (< 0), la risposta è sempre impostata per essere delimitata all'interno della curva iniziale; cioè il flag "/b" è attivo, indipendentemente dalla definizione dell'utente.
Forza iniziale (P0) e Rapporto di forza minima (Pa)
La forza iniziale P0 e la forza minima Pa sono state studiate per rappresentare la forza iniziale presente prima dell'inizio dei cicli, e una forza minima (attiva) sperimentata per uno spostamento negativo. Entrambe queste forze sono definite in funzione di Fy. P0 varia tra 0 P0 0.9. P0 > 0 sposta la curva dorsale verso il lato in trazione (a sinistra), e determina una forza iniziale in corrispondenza dello spostamento nullo. La forza minima Pa viene trattata come una linea di base del modello, e il movimento non va mai sotto questo livello. A Pa si applicano le seguenti condizioni: 0 Pa P0 ; Pa Fy ; Pa Fc.
Rapporto fattore forza scorrimento/taglio (fs)
Questo specifica l'inclusione di una forza di taglio laterale, che è definita come porzione di sdFc (si vedano i parametri ps e es nel seguito). Questo valore è preso in considerazione solo quando il flag "/s" è attivo, nel qual caso si assume che sia presente un taglio laterale e viene considerato fs al posto di Pa (cioè Pa=0 e l'asse degli spostamenti corrisponde alla linea di base). I limiti di fs sono i seguenti: 0 fs 0.9.
Fattore di rigidezza di scarico (
)
In funzione del flag "/a", può rappresentare un limite per il fattore di degrado/hardening della rigidezza di scarico (flag "/a" off) oppure può indicare, invece, un moltiplicatore costante della rigidezza di scarico (flag "/a" on). Quando il flag è attivo, varia come > 0; un valore di > 1 può essere usato per impostare la rigidezza di scarico maggiore della rigidezza iniziale della curva dorsale iniziale (il valore di default è comunque pari a 1).
Come specificato sopra, quando il flag è impostato su off, è usato come valore limite del fattore di rigidezza di scarico ciclico ku (si vedano i parametri pk ed ek nel seguito); per il degrado (pk<1), pk 1, mentre per l'hardening (pk>1), 1 pk.
Molti esperimenti non mostrano tipicamente valori di tanto più piccoli di uno, sebbene questo sia permesso dal modello. È anche importante notare che il valore di influenza la risposta, così calcolata, in maniera significativa, per cui è necessario prestare sufficiente attenzione nella scelta di questo valore; infatti una stima non realistica di può portare a risultati profondamente errati.
Parametri di degrado della rigidezza/resistenza (pk, ek, ps, es)
I parametri di rigidezza (pk, ek) e di resistenza (ps, es) sono impiegati per stimare il quantitativo di degrado della rigidezza e della resistenza durante i cicli di carico/scarico. Questi vengono poi utilizzati in una forma "indipendente dagli sforzi" dell'equazione di degrado "ellittica" fornita da Allotey and El Naggar [2005a; 2005b] per calcolare i fattori di degrado della rigidezza e della resistenza, ku e sd. Gli intervalli dei valori di questi parametri sono: pk>0, ek>0 e ps>0, es>0; il degrado è ottenuto quando pk o ps sono minori di 1, altrimenti viene applicato l'hardening. Per la maggior parte delle applicazioni pratiche, degrado o hardening avvengono in simultanea per rigidezza e resistenza (cioè è raro che il degrado della resistenza si verifichi contemporaneamente all'hardening della rigidezza, o viceversa); questo non è comunque applicato.
I fattori ku e sd sono calcolati sulla base di mezzo ciclo, e sono quindi valutati all'inizio di ogni scarico o ricarico. Questi valori vengono poi applicati alla curva dorsale originale per ottenere sia l'attuale curva standard di ricarico, sia la curva generale di scarico. Le seguenti limitazioni, alcune delle quali sono già state riscontrate, si applicano come condizioni limite per i valori di questi due fattori:
- per lo scarico, è tenuto in considerazione solo i degrado/hardening della rigidezza, e per tutti i casi sd=1
- per lo scarico, quando il flag "/a" è attivo, non avviene il degrado/hardening ciclico della rigidezza, e viene assunto un fattore di rigidezza costante, cioè ku =
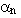
- per lo scarico, quando il flag "/a" non è attivo, 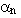rappresenta un valore massimo/minimo del degrado/hardening, cioè se pk<1 allora ku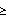 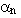, mentre se pk>1 allora ku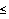
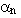
Nota: Per default, a tutti questi parametri è assegnato un valore pari a 1, che significa assenza di degrado/hardening.
Parametri della curva S-N (ks, f0)
La curva S-N descrive il rapporto dello sforzo ciclico (cioè il rapporto tra lo sforzo ciclico e lo sforzo effettivo medio iniziale 
) rispetto al numero di cicli di carico, simile a quello utilizzato per l'analisi a fatica. È impiegata per valutare il danno incrementale dovuto ad ogni mezzo ciclo di carico, al fine di stimare il degrado/hardening ciclico cumulativo all'inizio di ogni scarico o ricarico. Nel modello, la curva S-N è espressa come Sr = S/S1 rispetto al numero di cicli, dove S e S1 sono i fattori di sforzo per i cicli in corso e i primi cicli, rispettivamente. A disposizione dell'utente ci sono due diverse forme della curva S-N; se il flag "/logs" è attivo, è impiegata una relazione log-log, mentre se il flag "/logs" non è attivo, è considerata invece una relazione semi-log. Il parametro ks è la pendenza della curva S-N; per la relazione log-log, ks è uguale alla pendenza della curva S-N convenzionale (ksc), mentre per il caso semi-log, ks = ksc/S1 [si vedano Allotey and El Naggar, 2005a; 2005b].
Il parametro f0 è lo sforzo del suolo corrispondente a S1, cioè f0 = S1 (si noti che le unità di misura di devono essere consistenti con quelle di Fy). Il parametro varia come f0>0, con un valore di default f0=2Fy, e può essere regolato per tenere in considerazione gli effetti dello sforzo ciclico medio [e.g. Hyodo et al., 1994].
Parametri di fessurazione del suolo (p1, p2)
Il parametro della forza di apertura, p1, è impiegato per stimare il punto di ricarico diretto (fmm) a cui è diretta la curva di ricarico diretto (DRC). Il valore del parametro varia tra 0 <= p1 <= 1, con la DRC parallela all'asse degli spostamenti quando p1=0, come discusso in precedenza. Per il ricarico dopo il movimento lungo la linea di base, per il caso in cui il flag "/s" è attivo, questo si traduce nella formazione di una pura apertura. Il cambiamento dalla curva di ricarico diretto (RDC) alla curva di ricarico standard (SRC) avviene presso l'intersezione tra la RDC e l'attuale curva di ricarico standard alla base (B_SRC). Gli utenti dovrebbero riferirsi al lavoro di Allotey and El Naggar, 2005a; 2005b per ulteriori dettagli. Il valore predefinito è p1=0, cioè si presume un comportamento completamento non confinato (ciò potrebbe rappresentare, per esempio, una risposta "full gapping stiff clay-pile").
Il parametro p2 rappresenta l'effetto di "crollo del terreno", ed è impiegato per stimare lo spostamento iniziale, ds, dell'attuale B_SRC. Il parametro varia nel seguente modo: 0 <= p2, con p2=0, il che significa che nessuna caduta del suolo avrà luogo (cioè la curva B_SRC inizia dall'attuale punto di spostamento di scarico della linea di base); questa è l'ipotesi di default.
Impostazioni delle combinazioni Flag
Come descritto sopra, questa curva di risposta impiega cinque flag (/logS, /s, /b, /kbu, /a) che possono essere utilizzati per attivare o disattivare un numero uguale di funzionalità del modello, anch'esse descritte in precedenza. A ciascuno dei cinque flag può essere assegnato uno dei due stati mutuamente esclusivi (acceso (o) o spento (x)), quindi risulta evidente che all'utente sono rese disponibili ben 2^5=32 combinazioni possibili, come mostrato nella tabella sottostante. Per default, è impiegata la combinazione n°31, il che significa che tutti flag sono attivati, e cioè (i) è considerata una curva S-N log-log, (ii) è incluso il taglio laterale, (iii) la risposta è limitata, (iv) la rigidezza di scarico segue la curva dorsale, (v) non si verifica il degrado/hardening ciclico della rigidezza.
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
|
| /logS |
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
| /s |
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
o
|
| /b |
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
x
|
x
|
x
|
x
|
o
|
o
|
o
|
o
|
| /kbu |
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
x
|
x
|
o
|
o
|
| /a |
x
|
0
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
x
|
o
|
Note
- Questo versatile modello isteretico è ancora in fase di test e di ulteriori sviluppi. Per esempio, attualmente questa curva ssi_py è valido solo per la direzione forza-spostamento normale (cioè non tiene conto della risposta tangenziale forza-scorrimento). In aggiunta, o forse in tandem, il gradi di libertà non sono completamente accoppiati (una limitazione che è anche una conseguenza della natura attualmente disaccoppiata degli elementi link in SeismoStruct). Si prevede che entrambi questi temi saranno affrontati nelle prossime versioni di SeismoStruct.
- È molto probabile che le versioni future di SeismoStruct introdurranno un modo molto più "user-friendly" per calibrare/regolare i parametri di questa curva di risposta, con menu a discesa e/o pulsanti di opzione per selezionare le varie opzioni di modellazione.
- Negli ultimi anni, è stato proposto un approccio alternativo alla modellazione di sistemi di fondazione, che consiste nell'impiego di un macro-modello V-H-M completamente accoppiato [e.g. Cremer at al, 2002]. Esso utilizza un solo elemento per modellare l'intera risposta della fondazione e si basa su una "formulazione a plasticità della superficie di snervamento". Anche se questo è certamente un promettente approccio per la modellazione dell'interazione suolo-struttura, si ritiene che, allo stato attuale di sviluppo e di pratica, la più tradizionale procedura BNWF, attualmente implementata in SeismoStruct attraverso l'impiego della potente curva di risposta ssi_py, offra agli utenti tutte le funzioni necessarie per un'adeguata modellazione dell'interazione statica, e soprattutto dinamica, tra suolo, fondazioni e strutture.